Review sách “Mật mã - Từ cổ điển đến lượng tử” (Simon Singh)

Một trong những bài toán thú vị nhất của toán học đó bài toán dịch ngược. Nói một cách đơn giản đó là khi bạn đã biết kết quả của một quá trình tính toán nào đó và bạn muốn suy luận được ra cụ thể quá trình tính toán ấy như thế nào. Mã hóa và giải mã là những ví dụ điển hình cho bài toán tính toán xuôi chiều và bài toán dịch ngược (Direct problem and Inverse problem).

Bài toán dịch ngược nhìn chung rất khó giải quyết và có thể không chỉ có 1 lời giải duy nhất, trong khi đó bài toán tính toán xuôi chiều rất nhanh và dễ thực hiện. Ví dụ như khi ta nhân 2 số nguyên tố khá lớn (khoảng 450 chữ số chẳng hạn) thì ta được 1 số nguyên cực kỳ lớn. Rất khó để có thể phân tích số nguyên rất lớn đó ra thành 2 số nguyên tố ban đầu.

Cuốn sách viết về những vấn đề kể trên mà mình muốn giới thiệu ngày hôm nay là cuốn “Mật mã - Từ cổ điển đến lượng tử” của tác giả Simon Singh, một nhà văn, nhà sản xuất truyền hình nổi tiếng chuyên về lĩnh vực toán và khoa học. Cuốn sách được xuất bản năm 1999 (trùng với năm sinh của người viết bài :’>), sau thành công của cuốn sách trước đó của ông là cuốn “Định lý cuối cùng của Fermat” (1997). Cuốn sách dễ dàng lôi cuốn người đọc bởi cách dẫn dắt vấn đề rất khéo léo của Singh, trước khi đi đến bài toán kỹ thuật cụ thể, ông kể cho người đọc nghe về một câu chuyện lịch sử gắn với bài toán đó. Ông gieo vấn đề để người đọc suy nghĩ trước, đó là những mật mã khó mà tưởng chừng như không thể giải mã nổi, rồi sau đó ông lại tiếp tục kể câu chuyện lịch sử của mình, xen vào đó là lỗ hổng của mật mã dần được tìm ra và cuối cùng là cách giải mã nó.

Cuốn sách “Mật mã - Từ cổ điển đến lượng tử”

Cuốn sách bắt đầu với một câu chuyện ly kỳ về âm mưu Babington năm 1586, Nữ hoàng Mary của Scotland bị mang ra xét xử vì mưu đồ tạo phản, bà bị buộc tội đã âm mưu ám sát Nữ hoàng Elizabeth để cướp lấy vương miện nước Anh. Người của Elizabeth đã bắt chặn được những lá thư mà Mary gửi cho những kẻ mưu phản, có điều, những lá thư này đều đã được mã hóa. Nếu những lá thư này bị giải mã thì số phận của Mary coi như đã được định đoạt. Đây là những bước phát triển đầu tiên của mật mã, loại mật mã đơn giản nhất: mật mã thay thế dùng một bảng chữ cái (“monoalphabetic cipher”) , đó là cách làm xáo trộn nội dung bức thư bằng cách thay thế các chữ cái trong bức thư bằng các chữ cái tương ứng trong bảng chữ cái khác. Bước đột phá lớn nhất trong việc tìm ra cách phá giải loại mật mã này được tìm ra bởi vị triết gia Ả Rập Al-Kindi. Trong hơn 1000 năm, mật mã thay thế dùng một bảng chữ cái từng được coi là không thể phá giải nổi cho tới khi người ta tìm thấy những nghiên cứu của Al-Kindi. Phương pháp của Al-Kindi được gọi là phân tích tần suất, ông liệt kê số lần xuất hiện của tất cả các chữ cái trong bảng chữ cái, sắp xếp theo thứ tự giảm dần về số lần xuất hiện rồi đối chiếu lại với bảng tần suất xuất hiện các chữ cái của các văn bản thông thường, từ đó dựa vào sự giống nhau về tần suất cũng như suy luận về ngữ nghĩa các câu văn người giải mã có thể phá giải hoàn toàn văn bản mã hóa. Phương pháp này đã khiến cho những lá thư của Mary bị giải mã hoàn toàn và số phận của cô đã được định đoạt.

Nữ hoàng Mary xứ Scotland. Nguồn ảnh

Toán học và mật mã có sự liên quan mật thiết với nhau, theo dòng lịch sử, ta lại càng thấy rõ được điều đó. Sự xuất hiện của máy “Enigma” của quân đội Đức trước Chiến tranh Thế giới thứ hai khiến cho các nhà giải mã phải sử dụng những phương thức toán học mạnh để phá giải nó. Những nỗ lực đầu tiên đến từ những người Ba Lan, bắt đầu từ năm 1930, họ tuyển chọn một nhóm gồm 20 nhà toán học mà trong đó có Marian Rejewski, người đã tìm được ra cách phá giải mật mã “Enigma” với những chiếc máy “bombe” của mình. Ngay trước cuộc xâm lược của Đức quốc xã vào năm 1939, Ba Lan đã bí mật chuyển tới London phương pháp giải mã “Enigma”, cung cấp cho người Anh một chỉ dẫn quan trọng trong việc đánh bại phiên bản “Enigma” phức tạp hơn nhiều được sử dụng trong chiến tranh. Người tiên phong trong việc giải mã phiên bản “Enigma” phức tạp hơn này là Alan Turing.

Máy Enigma I dùng trong quân sự. Nguồn ảnh

Nhưng những điều kể trên vẫn chưa phải là phương pháp toán học gây bất ngờ và tuyệt vời nhất của mật mã học. Phương pháp mà Singh cho là “thành tựu lớn nhất của mật mã thay thế dùng một bảng chữ cái trong suốt 2000 năm”, đó là mật mã hóa khóa công khai. Nó dựa trên ý tưởng mang tính cách mạng rằng ta có thể công khai hoàn toàn cách thức mã hóa văn bản để mọi người có thể dựa vào đấy mà mã hóa văn bản của họ rồi gửi cho ta, văn bản mã hóa chỉ mình ta giải mã được vì ta là người duy nhất giữ khóa bí mật (“private key”). Nếu không biết khóa bí mật thì kẻ gian nếu có bắt chặn được văn bản thì cũng không thể giải mã dù biết rõ cách thức mã hóa. Lý thuyết đằng sau phương pháp mã hóa tuyệt vời này được Whitfield Diffie, Martin Hellman và Ralph Merkle công bố năm 1976.

Một trong những đặc điểm thú vị nhất của mật mã hóa khóa công khai đó là áp dụng một mảng thuần túy và ít ứng dụng nhất của toán học: lý thuyết số (“Number theory”). Lý thuyết số là một mảng nghiên cứu về các tính chất của tất cả các con số. Ví dụ như bất cứ số nguyên nào khi lũy thừa bậc 5 sẽ được một số nguyên có chữ số hàng đơn vị giống với chữ số hàng đơn vị của số nguyên ban đầu. Có điều hệ thống của Diffie-Hellman-Merkle khi đó mới dừng lại ở mức lý thuyết, chưa có một hệ thống thực nào chạy được cả. Đến năm 1977, ba nhà toán học của Viện Công nghệ Massachusetts là Ronald Rivest, Adi Shamir và Leonard Adleman đưa ra một phương pháp khéo léo để đưa hệ thống lý thuyết của Diffie-Hellman-Merkle đi vào thực tế, nay người ta vẫn hay gọi là giải thuật RSA. Chỉ với một chút kiến thức về lý thuyết số cùng với cách áp dụng khéo léo đã biến mớ lý thuyết trên giấy thành một doanh nghiệp với doanh thu hàng năm 200 triệu đô la, với hơn 300 triệu bản copy chương trình ứng dụng thuật toán RSA được cài đặt trên toàn thế giới.

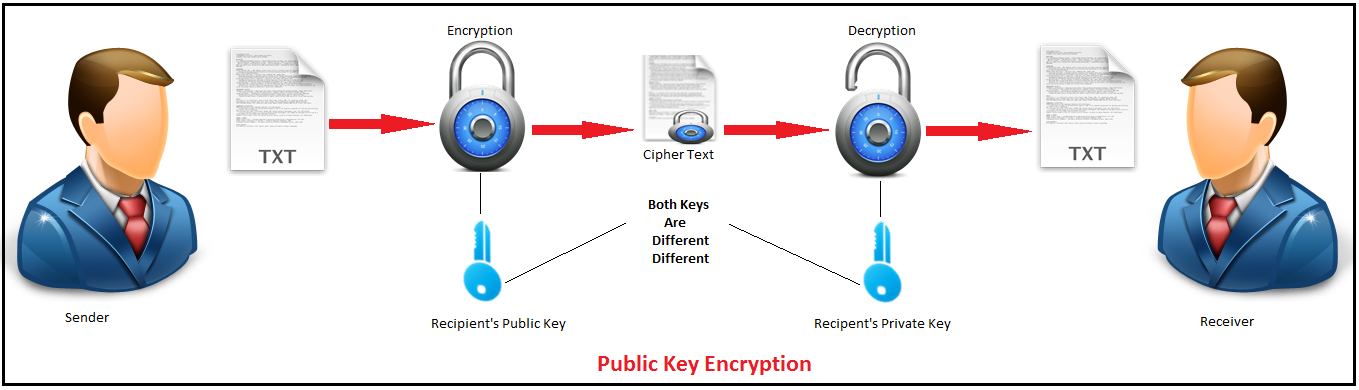
Sơ đồ nguyên lý của mật mã hóa khóa công khai. Nguồn ảnh

Theo dòng chảy của lịch sử thì đến đây dường như RSA đã trở thành loại mật mã không thể phá giải. Điều này bắt đầu gây ra mối lo ngại đối với các tổ chức chính phủ vì nếu mật mã quá mạnh thì họ sẽ mất đi khả năng kiểm soát thông tin. Chính phủ phải quyết định có nên sử dụng loại mật mã này hay không vì lợi ích là người dân có được sự riêng tư nhưng bên cạnh đó tội phạm có thể ngang nhiên sử dụng mật mã RSA để giao tiếp bí mật với nhau mà không bị phát hiện. Cơ quan An ninh Quốc gia của nhiều nước bắt đầu điều phối các quy định về mã hóa và giải mã, tích cực tuyển mộ các nhà toán học tài năng ở khắp nơi trên thế giới. Tất nhiên là Singh chỉ đề cập đến N.S.A (“National Security Agency”), vì đó là cơ quan ông nắm thông tin rõ nhất.

Trong chương cuối cùng, Singh đề cập đến một ứng cử viên nặng ký nhất, được coi là cú chốt hạ cho bên mã hóa: máy tính lượng tử và mã hóa lượng tử. Mã hóa lượng tử nghe như một bộ phim khoa học viễn tưởng, nhưng thực ra có một nền tảng khoa học vững chắc đằng sau nó. Bên cạnh đó, Singh còn kể về một câu chuyện vừa thực vừa ảo về một công cuộc giải mã để tìm ra vị trí “đảo giấu vàng”: mật mã Beale (đây là 1 câu chuyện lý thú, bạn có thể tìm kiếm từ khóa “Beale ciphers” nếu không có điều kiện đọc sách). Ngoài ra, Singh còn chia sẻ những câu chuyện về khảo cổ học, những cách khéo léo tài tình của con người hiện đại trong việc giải mã các ký tự cổ xưa: Thomas Young với việc giải mã Phiến đá Rosetta; những kỳ tích của Jean-Francois Champollion trong việc phá giải các chữ tượng hình của người Ai Cập cổ đại hay việc tìm ra bí mật của Linear B. Đó là những câu chuyện tuyệt vời và ly lỳ nhất trong lịch sử mật mã học.

Mảnh đất sét chứa những bản khắc của Linear B. Nguồn ảnh

Trong mỗi chương của cuốn sách, Simon Singh đã trình bày những điểm nổi bật nhất trong lịch sử mật mã học, người đọc dù là người chưa biết gì về mật mã, hay người đã có kiến thức về mật mã đều có thể đọc được, tác giả luôn đi từ câu chuyện lịch sử rồi mới diễn giải các vấn đề kỹ thuật một cách dễ hiểu. Singh còn để lại cho độc giả một Thách thức Giải mã trị giá 10 ngàn đô la cho ai giải mã được hết 10 văn bản mã hóa ở cuối sách. Bạn đọc có thể tham khảo thông tin trên website của tác giả: simonsingh.net/cryptography/cipher-challenge/

Tác giả Simon Singh. Nguồn ảnh

Nếu có điều kiện, hãy cố gắng tìm đọc cuốn sách thú vị này nhé, chúc bạn một ngày tốt lành ! :)